Le cône impossible, aussi appelé impossible cone en anglais, est un objet fascinant à la…

Entrons dans le monde fascinant des objets mathématiques pour explorer ensemble l’un des joyaux de la géométrie : l’icosaèdre.
C’est une forme qui, malgré sa simplicité apparente, cache une richesse incroyable de propriétés et d’applications.
Qu’est-ce que l’icosaèdre ?
L’icosaèdre est une forme pure, un solide qui appartient à la famille prestigieuse des Solides de Platon.
Il se distingue par sa symétrie, sa beauté et sa structure, composée de 20 faces équilatérales, 30 arêtes et 12 sommets.
De plus, c’est un polyèdre régulier, ce qui signifie que toutes ses faces sont identiques et ses sommets sont équidistants.
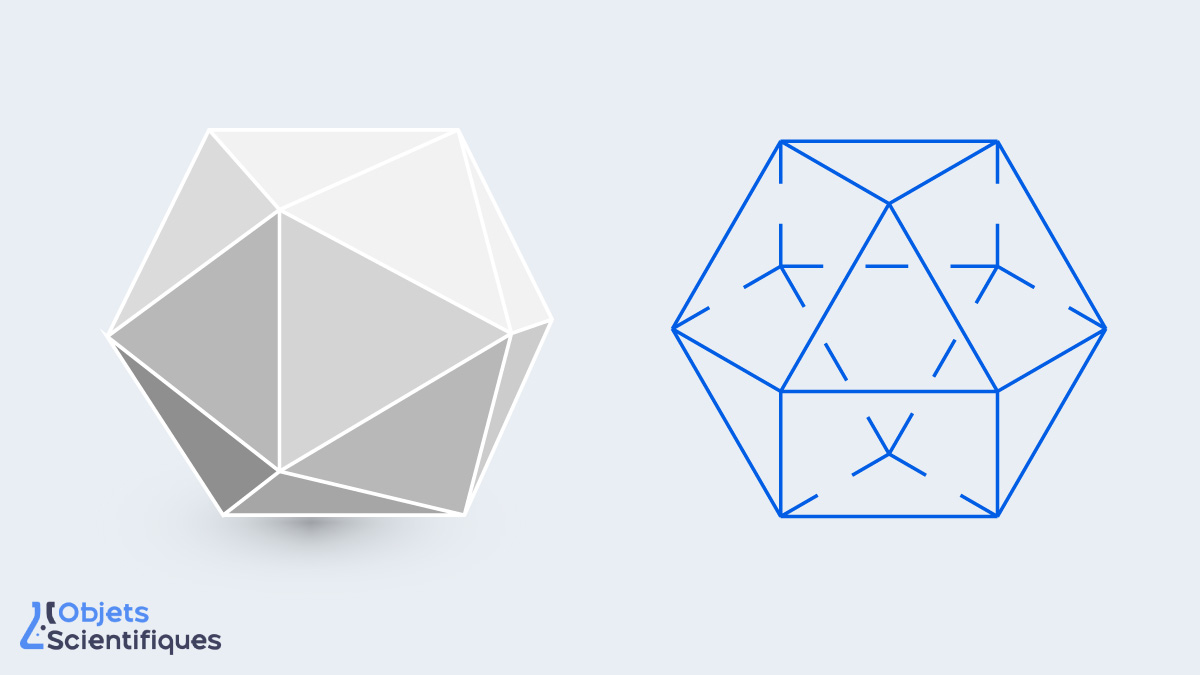
Importance géométrique et symbolique de l’icosaèdre
Pourquoi est-il si important en géométrie ? Sa symétrie parfaite et sa structure harmonieuse en font un objet d’étude fascinant.
En outre, il est lié au nombre d’or, ce ratio universel qui apparaît partout dans la nature, de la forme d’un coquillage à la disposition des graines de tournesol.
Mais l’icosaèdre n’est pas seulement un objet de curiosité géométrique.
Sa beauté et sa symétrie lui ont également conféré une grande signification symbolique à travers les âges.
Pour les Grecs anciens, il représentait l’élément de l’eau. Dans les cultures modernes, il est souvent associé à l’harmonie et à l’équilibre.
Ce voyage que nous allons entreprendre dans l’univers de l’icosaèdre promet d’être riche en découvertes.
Alors, accrochez-vous, car nous allons plonger dans le monde fascinant de ce polyèdre unique.
Origine et Histoire
Les Solides de Platon
La première rencontre avec l’icosaèdre nous ramène à l’antiquité grecque.
Il fait partie des Solides de Platon. Mais qui sont-ils ?
Ces cinq polyèdres réguliers ont des faces, des arêtes et des sommets identiques. La beauté de leur symétrie a intrigué les mathématiciens depuis l’Antiquité.
Le saviez-vous ? Les Solides de Platon tirent leur nom du philosophe grec Platon. Il les a associés aux éléments de la nature : le tétraèdre à feu, le cube à la terre, l’octaèdre à l’air, l’icosaèdre à l’eau et le dodécaèdre à l’univers.

Les solides de Platon sont cinq polyèdres réguliers convexes, à savoir le tétraèdre, le cube, l’octaèdre, le dodécaèdre et l’icosaèdre, dont chaque face est un polygone régulier identique et dont les angles entre chaque paire de faces sont égaux.
L’icosaèdre à travers l’histoire
L’icosaèdre a une riche histoire. Depuis l’antiquité, il a été un symbole d’harmonie et d’équilibre.
Chez les Grecs, il représentait l’eau, un des quatre éléments fondamentaux.
Au Moyen Âge, le mystique Johannes Kepler l’a utilisé dans son modèle de l’univers.
Il pensait que les orbites des six planètes connues à l’époque étaient délimitées par les cinq Solides de Platon, dont l’icosaèdre.

Aujourd’hui, l’icosaèdre est un outil précieux en mathématiques, en physique et même en biologie.
Par exemple, de nombreux virus ont une structure icosaédrique, ce qui permet une organisation optimale de leur matériel génétique.
Et saviez-vous que l’icosaèdre est aussi un objet d’art et de décoration ? Sa forme élégante et harmonieuse le rend parfait pour des sculptures, des bijoux, et même des jeux de société !
Voilà un aperçu de la façon dont l’icosaèdre a imprégné notre histoire, notre science et notre culture.
Propriétés de l’Icosaèdre
Définition et description de l’icosaèdre
C’est un polyèdre régulier qui fait partie des cinq Solides de Platon.
Sa forme est ronde et presque sphérique, ce qui le rend particulièrement esthétiquement plaisant.
Et devinez quoi ? Le mot « icosaèdre » vient du grec « eíkosi« , qui signifie « vingt« , et « hédra« , qui signifie « siège » ou « face« .
Donc, l’icosaèdre est un solide avec vingt faces!
Ses éléments : sommets, arêtes, faces
Chaque icosaèdre possède 20 faces, 30 arêtes et 12 sommets. Chaque face est un triangle équilatéral identique.
De plus, cinq arêtes se rencontrent à chaque sommet. C’est la symétrie qui donne à l’icosaèdre sa beauté intemporelle.
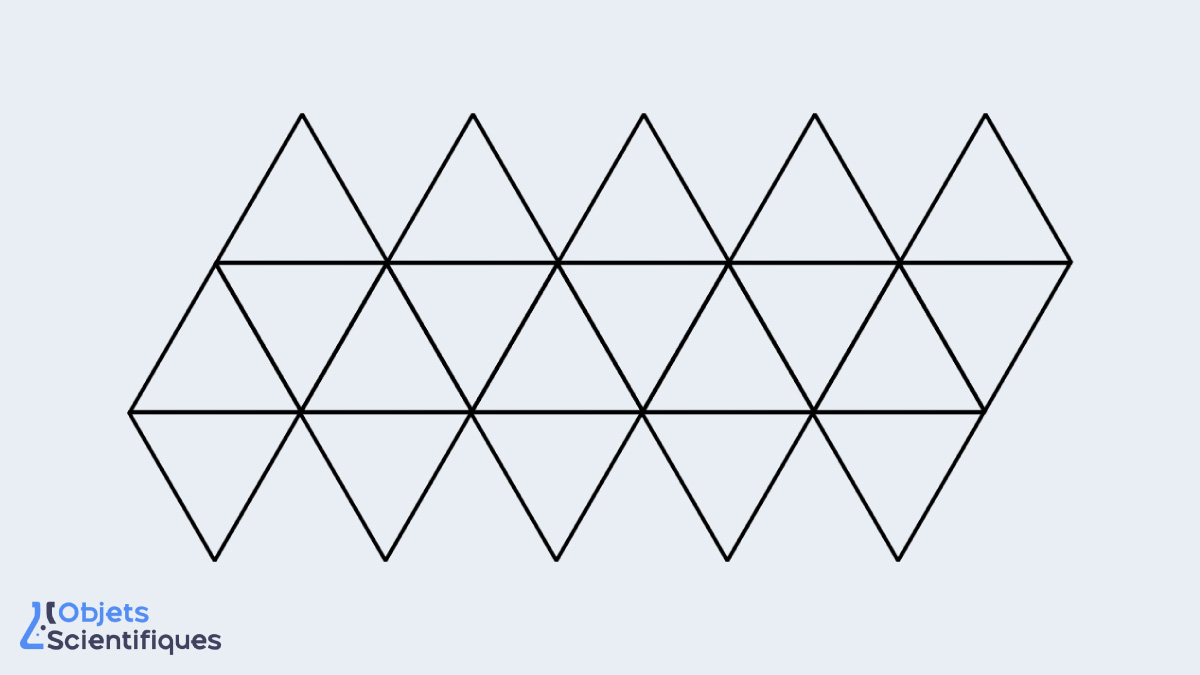
Relations entre ces éléments
Maintenant, entrons dans le détail. Les sommets de l’icosaèdre sont disposés en trois anneaux horizontaux.
Le ring du haut et du bas contient chacun cinq sommets. Le ring du milieu, le plus large, contient deux fois plus de sommets.
Et les arêtes? Chaque arête est partagée par deux triangles adjacents.
Si vous suivez une arête, vous découvrirez qu’elle vous conduit à un sommet, puis à une autre arête, et ainsi de suite.
Quant aux angles, chaque angle formé par deux arêtes est le même, peu importe où vous le mesurez sur l’icosaèdre. C’est cette égalité qui assure la régularité du solide.
En géométrie
La symétrie de l’icosaèdre est impressionnante. Il a 15 axes de rotation: 10 passent par les paires de sommets opposés, 5 par les paires de faces opposées.
Ainsi, l’icosaèdre peut être tourné de nombreuses façons sans changer d’apparence.
Et que dire des angles diédraux? C’est l’angle formé par deux faces adjacentes. Pour l’icosaèdre, cet angle est d’environ 138,19 degrés.
Voilà donc pour les propriétés fondamentales de l’icosaèdre. Comme vous pouvez le constater, ce n’est pas seulement un objet de beauté, mais aussi un trésor géométrique.

Icosaèdre et nombre d’or
Présence du nombre d’or
Le nombre d’or, connu aussi sous le nom de Phi (∅), est un invité surprise dans notre histoire de l’icosaèdre. Il joue un rôle clé dans la géométrie de ce solide platonique (platonicien).
Le rapport entre la longueur de l’arête et le rayon de la sphère circonscrite de l’icosaèdre est exactement le nombre d’or.
Il souvent appelé divine proportion, est un nombre irrationnel défini pour la première fois par Euclide vers 300 avant J.C. comme le « partage d’une droite en moyenne et extrême raison ».
Sa valeur est environ 1,61803398875, obtenue par la formule 1+√5 sur 2, et il peut aussi être exprimé par l’équation algébrique x2 = x+1.
Triangles et rectangles d’or
Si vous observez attentivement un icosaèdre, vous découvrirez de nombreux triangles et rectangles d’or.
Par exemple, prenez deux faces contiguës. Les quatre sommets de ces faces forment un rectangle d’or.
Le rapport entre la longueur et la largeur de ce rectangle est exactement le nombre d’or!
Quant aux triangles, chacun des 20 triangles équilatéraux qui composent l’icosaèdre est un triangle d’or.
Si vous tracez une ligne du sommet à la base, vous obtenez un triangle dont le rapport entre la base et la hauteur est égal au nombre d’or.
L’icosaèdre et le pentagone
L’histoire de l’icosaèdre et du pentagone est un chapitre fascinant de la géométrie.
Si vous dessinez un pentagone autour de chaque sommet de l’icosaèdre, vous obtenez un dodécaèdre, le dual de l’icosaèdre.
Plus encore, si vous joignez les milieux des faces de l’icosaèdre, vous obtenez un autre pentagone, mais cette fois dans un espace tridimensionnel.
Le lien entre l’icosaèdre et le pentagone n’est pas seulement esthétiquement plaisant, il révèle aussi l’harmonie profonde qui régit les solides de Platon.
Dualité de l’Icosaèdre
Dualité dans les polyèdres
L’un des concepts les plus captivants dans l’étude des polyèdres est la dualité.
Deux polyèdres sont dits duaux si les sommets de l’un correspondent aux faces de l’autre, et vice versa.
La relation de dualité révèle une profonde symétrie entre ces objets géométriques.
Le dodécaèdre comme dual de l’icosaèdre
L’icosaèdre, notre héros géométrique, a un jumeau dans le monde des polyèdres : le dodécaèdre. Le dodécaèdre est le dual de l’icosaèdre.
Il est composé de 12 faces pentagonales régulières. Chaque face du dodécaèdre correspond à un sommet de l’icosaèdre, et chaque sommet du dodécaèdre correspond à une face de l’icosaèdre.
Les symétries et isométries des duaux
L’icosaèdre et son dual, le dodécaèdre, partagent un grand nombre de symétries et isométries.
Cela signifie que vous pouvez tourner, refléter ou autrement manipuler ces formes d’une certaine manière sans changer leur apparence globale.
Pour l’icosaèdre, chaque rotation ou réflexion qui le laisse invariant laisse également invariant l’ensemble des centres de ses faces.
Par conséquent, toute symétrie de l’icosaèdre est aussi une symétrie du dodécaèdre. Le même raisonnement montre que toute symétrie du dodécaèdre est aussi une symétrie de l’icosaèdre.
Caractéristiques de l’Icosaèdre
Dimensions caractéristiques
L’icosaèdre a de nombreuses dimensions caractéristiques qui contribuent à sa beauté et à son harmonie géométrique.
Parmi elles, on retrouve la longueur de l’arête, l’angle diédral et les rayons des sphères inscrite et circonscrite.
Les rapports entre dimensions
L’icosaèdre est un trésor de rapports entre dimensions. Par exemple, le rayon de la sphère circonscrite est environ 0,95 fois la longueur de l’arête, tandis que le rayon de la sphère inscrite est d’environ 0,76 fois cette même longueur.
Ces ratios, et bien d’autres, contribuent à la structure unique de l’icosaèdre.
L’icosaèdre dans une sphère
On peut inscrire un icosaèdre dans une sphère. La sphère circonscrite touche l’icosaèdre en ses 12 sommets, tandis que la sphère inscrite est tangente à l’icosaèdre sur les faces. Le volume de l’icosaèdre est environ 0,61 fois le volume de la sphère circonscrite.
Ce ratio est une autre manifestation de l’harmonie géométrique de l’icosaèdre.
Ses applications et ses utilisations
L’icosaèdre en art et architecture
En raison de sa beauté géométrique, l’icosaèdre a été une source d’inspiration pour les artistes et les architectes à travers l’histoire.
Ses formes triangulaires et sa symétrie ont été utilisées dans des sculptures, des bijoux et des bâtiments.
Il existe même des constructions architecturales modernes qui reposent sur l’icosaèdre comme unité de base.
Applications en mathématiques et physique
Dans les sciences, l’icosaèdre joue un rôle significatif. En mathématiques, il est utilisé dans l’étude de la théorie des groupes et de la géométrie.
En physique, des structures microscopiques, comme certains virus et minéraux, ont la forme d’un icosaèdre.
L’icosaèdre en informatique et modélisation 3D
L’icosaèdre est également essentiel dans l’informatique et la modélisation 3D. Il sert de base pour la création de sphères et d’autres formes en 3D.
Les modèles numériques de terrain, utilisés en cartographie et en jeux vidéo, exploitent souvent l’icosaèdre pour une représentation précise et équilibrée du terrain.
Comparaison des Solides de Platon
Voici un aperçu succinct des caractéristiques principales de chaque solide de Platon, incluant leur polyèdre dual.
| Solide de Platon | Nombre de Faces | Type de Faces | Nombre de Sommets | Nombre d’Arêtes | Polyèdre Dual |
|---|---|---|---|---|---|
| Tétraèdre | 4 | Triangles | 4 | 6 | Tétraèdre |
| Cube | 6 | Carrés | 8 | 12 | Octaèdre |
| Octaèdre | 8 | Triangles | 6 | 12 | Cube |
| Dodécaèdre | 12 | Pentagones | 20 | 30 | Icosaèdre |
| Icosaèdre | 20 | Triangles | 12 | 30 | Dodécaèdre |
Fondements de la Géométrie Sacrée
La géométrie sacrée inclut les solides platoniciens, des polyèdres convexes définis par Platon. Les tétraèdres, octaèdres, et autres forment ces polyèdres.
Chaque solide platonicien possède un même nombre de faces isométriques. Ces faces peuvent être des triangles, des carrés ou des pentagones réguliers.
Un prisme est un polyèdre dont deux faces sont des polygones identiques et parallèles, reliées par des faces carrées.
Une pyramide, à la différence du prisme, a une base polygonale et des faces triangulaires. Ces solides illustrent le concept de pavage, qui est l’intersection de plans dans l’espace.
La formule d’Euler, proposée par le mathématicien suisse, établit une relation entre le nombre de sommets, d’arêtes et de faces d’un polyèdre convexe. Le théorème de Pythagore, quant à lui, s’applique à des triangles isocèles dans ces solides.
Enfin, des patrons peuvent être créés pour chaque solide, en déroulant chaque face sur un plan. Ces patrons facilitent la compréhension de la somme des angles internes de chaque solide.
Conclusion
L’icosaèdre est plus qu’une simple forme géométrique; il est un symbole de beauté mathématique et un outil précieux pour la science et l’art.
Sa présence dans notre culture atteste de son influence, de l’architecture à la joaillerie, de la sculpture à la modélisation 3D.
Sa symétrie parfaite et sa relation étroite avec le nombre d’or lui confèrent une place privilégiée dans le domaine des mathématiques.
En physique, la forme de l’icosaèdre émerge naturellement dans des structures allant des cristaux aux virus.
Le monde numérique, en constante évolution, a trouvé de nouvelles utilisations pour l’icosaèdre.
La modélisation 3D, par exemple, utilise l’icosaèdre comme une base pour la construction de formes complexes.
En définitive, l’icosaèdre, avec ses vingt faces triangulaires et sa symétrie irréprochable, continue d’inspirer et de fasciner.
Il est un véritable témoignage de l’union entre l’art et la science, un lien entre le concret et l’abstrait, une preuve que la beauté peut naître de la pure logique mathématique.
Combien de sommets possède l'icosaèdre ?
L'icosaèdre a 12 sommets et 30 arêtes.
Où voit-on l'icosaèdre dans la nature ?
On trouve des icosaèdres dans la structure de certains virus et cristaux.
Comment construire un icosaèdre ?
Il faut assembler 20 triangles équilatéraux de manière symétrique. Un modèle en papier peut aider à visualiser la structure.
Qu'est-ce que le nombre d'or dans l'icosaèdre ?
Le nombre d'or apparaît dans les rapports de longueur entre les arêtes et les diagonales de l'icosaèdre.
Comment l'icosaèdre est-il utilisé en informatique ?
En informatique, l'icosaèdre est souvent utilisé dans la modélisation 3D et la génération de maillages.
Quel est le lien entre l'icosaèdre et le dodécaèdre ?
L'icosaèdre et le dodécaèdre sont des formes duales. Le centre de chaque face du dodécaèdre forme un sommet de l'icosaèdre et vice versa.
Quelle est l'importance de l'icosaèdre en art et en architecture ?
L'icosaèdre est apprécié pour sa symétrie parfaite. Il inspire les architectes et les artistes pour créer des œuvres esthétiques et harmonieuses.
Quels sont les bénéfices d'étudier l'icosaèdre ?
L'étude de l'icosaèdre développe notre compréhension de la géométrie et de la symétrie. Elle a aussi des applications concrètes en science, art et technologie.





Comments (0)