Force de Lorentz Expliquée – Un Guide Complet en Physique Électromagnétique

La force de Lorentz est un pilier fondamental de l’électromagnétisme qui joue un rôle important dans notre compréhension de l’univers physique.

Elle décrit l’interaction entre les particules chargées et les champs électromagnétiques, offrant une fenêtre sur des phénomènes aussi variés que le mouvement des électrons dans un circuit et les aurores boréales.

Cette force, éponyme du physicien Hendrik Lorentz, se manifeste à travers deux composantes distinctes : l’une électrique et l’autre magnétique.

Son étude éclaire non seulement les principes de base de la physique, mais aussi des applications pratiques allant des technologies quotidiennes aux expériences en physique des particules.

Dans cet article, nous explorerons la force de Lorentz, en détaillant sa nature, ses applications et son importance dans le vaste domaine de la physique, avec une attention particulière portée à sa formulation mathématique et à son intégration dans le cadre plus large de l’électrodynamique et de la relativité restreinte.

Qu’est-ce que la Force de Lorentz ?

La force de Lorentz ou force électromagnétique représente un concept essentiel en physique. Elle décrit comment les particules chargées interagissent avec les champs électriques et magnétiques.

Cette force se manifeste de deux manières : une composante électrique et une autre magnétique. C’est la force électrique qui agit sur une charge immobile, tandis que la composante magnétique influence les charges en mouvement.

En physique, la force de Lorentz se révèle cruciale pour comprendre les phénomènes électromagnétiques. Elle joue un rôle fondamental dans le mouvement des électrons dans les circuits électriques, l’alignement des aiguilles de boussoles, et même dans la formation des aurores boréales.

En chimie, cette force intervient dans les réactions électrochimiques et influence la structure des atomes. Elle aide à expliquer le comportement des électrons dans les liaisons chimiques.

Dans l’interaction électromagnétique, la force de Lorentz se positionne comme un pilier central. Elle illustre l’interaction entre la matière et les champs électromagnétiques, un aspect fondamental pour l’étude de l’univers à l’échelle microscopique et macroscopique.

En somme, cette force est un élément clé pour déchiffrer le comportement des particules chargées dans divers contextes naturels et technologiques.

Fondements Théoriques

Au cœur de la compréhension moderne de la physique, la force de Lorentz se révèle être un concept fondamental. nous allons plonger dans les fondements théoriques, explorant les principes qui gouvernent cette force.

Nous examinerons les champs électriques et magnétiques, des entités invisibles mais puissantes qui régissent les interactions des particules chargées. Ces champs ne sont pas seulement des abstractions mathématiques ; ils ont des effets concrets et mesurables sur la matière.

Nous aborderons ensuite les équations de Maxwell, pierre angulaire de l’électromagnétisme. Ces équations ne se contentent pas de décrire les champs ; elles révèlent l’interdépendance profonde entre l’électricité et le magnétisme.

Champs Électriques et Magnétiques

Dans l’univers de l’électromagnétisme, les champs électriques et magnétiques jouent des rôles clés. Le champ électrique, une force invisible, émane des charges électriques et agit sur d’autres charges à distance.

Sa nature est telle qu’une charge électrique crée un champ autour d’elle, influençant ainsi les particules chargées environnantes. Le champ magnétique, quant à lui, est une conséquence du mouvement des charges. Il se manifeste autour des aimants permanents ou des courants électriques.

Ces deux champs ne sont pas isolés ; ils interagissent constamment. Leurs interactions avec les particules chargées sont au cœur de la force de Lorentz. Un champ électrique exerce une force directe sur une charge, modifiant son mouvement.

Par contraste, un champ magnétique affecte une charge en mouvement, altérant sa trajectoire sans changer sa vitesse. Ces interactions fondamentales sont essentielles pour comprendre des phénomènes allant des circuits électriques aux communications sans fil.

En résumé, les champs électriques et magnétiques, bien que non perceptibles visuellement, sont omniprésents et essentiels à la dynamique des particules chargées dans notre monde.

Équations de Maxwell

Les équations de Maxwell constituent la pierre angulaire de notre compréhension de l’électromagnétisme. Formulées par James Clerk Maxwell au XIXe siècle, elles décrivent comment les champs électriques et magnétiques se propagent et interagissent.

Ces équations révèlent que les champs électriques et magnétiques ne sont pas statiques ; ils varient dans le temps et l’espace, influençant et étant influencés par les charges et les courants.

Le rôle de ces équations dépasse la simple description des champs. Elles unifient l’électricité et le magnétisme en une seule théorie cohérente, montrant que les variations du champ magnétique peuvent créer des champs électriques, et vice-versa.

Cette interdépendance est fondamentale dans la compréhension des ondes électromagnétiques, comme la lumière.

Le lien avec la force de Lorentz est direct et profond. Les équations de Maxwell fournissent le cadre nécessaire pour comprendre comment les champs électriques et magnétiques agissent sur les particules chargées.

La force de Lorentz, avec sa composante électrique agissant sur les charges immobiles et sa composante magnétique influençant les charges en mouvement, trouve son explication dans ce cadre.

Ainsi, les équations de Maxwell ne sont pas seulement des formules ; elles sont la clé pour déchiffrer un large éventail de phénomènes électromagnétiques dans l’univers.

Description Mathématique

La force de Lorentz se démarque par sa précision mathématique, offrant une compréhension claire des interactions électromagnétiques. Dans cette partie, nous parlerons de l’élégance mathématique qui sous-tend ce concept.

Nous détaillerons la formule fondamentale qui définit la force de Lorentz, mettant en lumière la relation entre les particules chargées, les champs électriques et magnétiques.

Chaque symbole et chaque terme de cette formule recèle une signification profonde, révélant comment les forces agissent et se transforment. Cette section ne se contente pas de présenter des équations ; elle vise à décrypter leur sens pour une compréhension approfondie.

Que vous soyez un étudiant en physique, un ingénieur, ou simplement un curieux des mystères de l’univers, cette exploration mathématique vous fournira les clés pour appréhender l’un des principes les plus fascinants de la physique moderne.

Formule de la Force de Lorentz

La formule de la force de Lorentz est une expression mathématique élégante, capturant l’essence des interactions électromagnétiques. Elle s’écrit :

F = q(E + v x B)

Chaque symbole dans cette formule porte une signification précise :

• F représente la force de Lorentz agissant sur la particule.
• q est la charge électrique de la particule.
• E désigne le champ électrique.
• v est la vitesse de la particule chargée.
• B symbolise le champ magnétique.
• Le symbole x indique un produit vectoriel, illustrant l’interaction entre la vitesse et le champ magnétique.

Cette formule révèle comment la force varie en fonction de la charge, de la vitesse, et des champs électrique et magnétique présents. Elle montre que la force dépend non seulement de l’intensité des champs, mais aussi de la direction de la vitesse de la particule.

En somme, cette expression mathématique ne se limite pas à décrire un phénomène ; elle éclaire le comportement dynamique des particules chargées dans des environnements électromagnétiques variés.

Composantes de la Force

La force de Lorentz se décompose en deux composantes fondamentales : l’électrique et la magnétique.

Chacune influence le mouvement des particules chargées de manière distincte.

Composante Électrique

La composante électrique de la force de Lorentz s’exprime par qE. Ici, q représente la charge de la particule et E le champ électrique. Cette force agit sur une particule chargée indépendamment de son mouvement.

Elle est directement proportionnelle à l’intensité du champ électrique et à la charge de la particule.

Dans un champ électrique, une charge positive est attirée vers la zone de potentiel électrique plus bas, tandis qu’une charge négative est attirée vers la zone de potentiel plus élevé.

Composante Magnétique

La composante magnétique, exprimée par q(v x B), dépend de la vitesse v de la particule et du champ magnétique B. Le symbole x indique un produit vectoriel, montrant que cette force est perpendiculaire à la fois à la vitesse de la particule et au champ magnétique.

En conséquence, contrairement à la composante électrique, la force magnétique ne fait pas varier la vitesse de la particule, mais modifie sa direction.

Ce phénomène est à l’origine de trajectoires courbées ou circulaires dans les applications telles que les cyclotrons.

Ces deux composantes illustrent la dualité et la complémentarité dans l’interaction des particules chargées avec les champs électromagnétiques, révélant la complexité et la richesse de la force de Lorentz.

Cas Particuliers

La force de Lorentz agit différemment selon l’état de la charge : en mouvement ou immobile.

Cette distinction apporte un éclairage sur la dynamique des particules chargées dans divers contextes.

Charge en Mouvement

Lorsqu’une charge est en mouvement, elle subit à la fois les composantes électrique et magnétique de la force de Lorentz. La composante électrique qE agit en fonction de l’intensité du champ électrique.

La composante magnétique, q(v x B), est cruciale : elle est perpendiculaire à la vitesse v et au champ magnétique B.

Cette force magnétique crée une trajectoire courbée pour la charge, essentielle dans des dispositifs comme les accélérateurs de particules.

Charge Immobile

Pour une charge immobile, la situation se simplifie. La composante magnétique de la force de Lorentz disparaît, car elle dépend de la vitesse de la particule. Ainsi, une charge immobile dans un champ magnétique ne subit aucune force magnétique.

Cependant, elle reste soumise à la force électrique si un champ électrique est présent. Ce cas souligne l’influence directe et immédiate du champ électrique sur les charges statiques.

Ces cas particuliers de la force de Lorentz illustrent la variété des interactions possibles entre les particules chargées et les champs électromagnétiques, reflétant la complexité et la diversité des phénomènes naturels et technologiques.

Applications Pratiques

La force de Lorentz transcende la théorie pour influencer de nombreux aspects de notre vie quotidienne et de la science moderne.

Elle se manifeste à la fois à des échelles macroscopiques et microscopiques, illustrant sa polyvalence.

Effets Macroscopiques et Microscopiques

Dans la vie quotidienne, les effets de la force de Lorentz sont omniprésents, bien que souvent invisibles. Par exemple, dans les haut-parleurs, les interactions entre champs magnétiques et courants électriques produisent des sons.

Sur le plan microscopique, cette force est essentielle dans les technologies d’imagerie médicale, comme l’IRM, où elle aide à créer des images détaillées des tissus internes du corps.

Dans le domaine scientifique et technologique, la force de Lorentz est un moteur d’innovation. Elle est au cœur du fonctionnement des accélérateurs de particules, permettant aux chercheurs de sonder la structure fondamentale de la matière.

Phénomènes Physiques

La circulation des courants électriques dans les câbles et circuits est un exemple classique de l’application de la force de Lorentz. Elle influence le chemin des électrons, jouant un rôle crucial dans la distribution et l’utilisation de l’électricité.

Dans les accélérateurs de particules, le mouvement des particules chargées est directement influencé par la force de Lorentz.

Cette force est utilisée pour accélérer, ralentir ou changer la direction des particules, permettant des découvertes révolutionnaires en physique des particules et en cosmologie.

Règle de la Main Droite

La règle de la main droite est une méthode mnémotechnique utilisée en physique pour déterminer la direction de certaines grandeurs en électromagnétisme. En particulier, elle est employée pour identifier l’orientation de la force de Lorentz, qui agit sur une particule chargée se déplaçant dans un champ magnétique.

Pour appliquer cette règle, on procède comme suit :

1. Alignement du Pouce : Le pouce de la main droite est aligné avec le vecteur de la vitesse de la particule chargée, c’est-à-dire dans la direction du mouvement de la charge.
2. Alignement de l’Index : L’index pointe dans la direction du champ magnétique. Si le champ est horizontal et pointe vers l’est, l’index serait dirigé horizontalement vers la droite.
3. Alignement du Majeur : Le majeur est placé perpendiculairement aux deux autres doigts, formant un angle droit avec le pouce et l’index. Il indiquera alors la direction de la force de Lorentz.

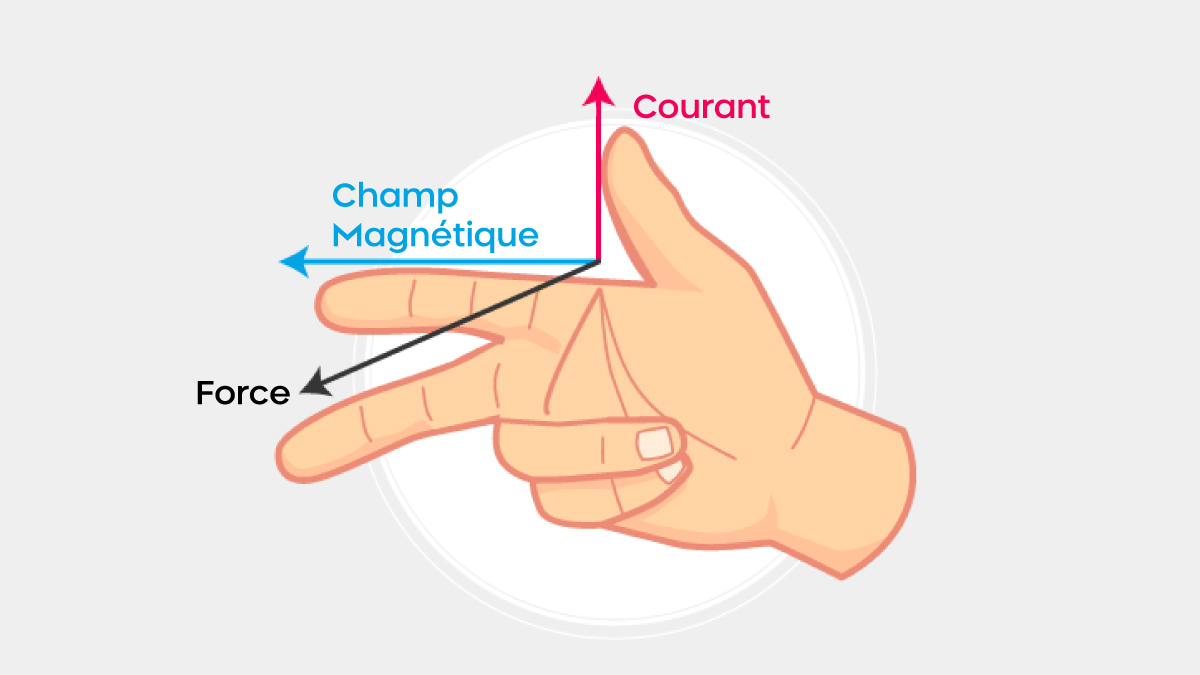
D’après la figure ci-dessus, on comprend que la force magnétique est perpendiculaire à la fois au champ magnétique et à la vitesse de la charge.

Électrodynamique Quantique

La force de Lorentz trouve une nouvelle dimension dans le monde de la mécanique quantique, explorée par l’électrodynamique quantique.

Cette branche de la physique fusionne les principes quantiques avec l’électromagnétisme, ouvrant un champ de compréhension plus profond.

Interaction avec la Mécanique Quantique

Dans l’électrodynamique quantique, la force de Lorentz n’est pas seulement une interaction entre particules chargées et champs classiques.

Elle devient une partie d’un tissu complexe d’échanges d’énergie et de quantas de lumière (photons). Les électrons et autres particules chargées échangent des photons, modifiant ainsi leurs trajectoires et énergies.

Cette interaction quantique révèle des aspects fascinants, comme l’effet tunnel et l’entanglement quantique.

Effets Quantiques sur la Force Électromagnétique

Les effets quantiques introduisent des nuances subtiles dans le comportement de la force électromagnétique. Par exemple, à cette échelle, les particules ne suivent pas des trajectoires déterministes mais probabilistes.

De plus, des phénomènes comme l’électrodynamique des champs confinés montrent que les propriétés des champs électriques et magnétiques peuvent varier considérablement à l’échelle quantique.

L’intégration de la force de Lorentz dans l’électrodynamique quantique enrichit notre compréhension des interactions fondamentales.

Elle souligne l’interconnexion profonde entre les théories classiques et quantiques, un domaine toujours en expansion et source d’innovations scientifiques.

Implications Théoriques

La force de Lorentz trouve des implications profondes dans des domaines théoriques avancés, enrichissant notre compréhension de la physique.

Relativité Restreinte et Force de Lorentz

La relativité restreinte d’Einstein apporte une perspective nouvelle à la force de Lorentz. Cette théorie montre que le temps et l’espace ne sont pas absolus, mais relatifs à l’observateur.

Dans ce cadre, la force de Lorentz se dérive en tenant compte de ces relativités. Elle implique l’utilisation du tenseur électromagnétique et de la quadrivitesse, des concepts qui relient les champs électriques et magnétiques à la structure de l’espace-temps.

Formalisme Lagrangien

Le formalisme Lagrangien, un pilier de la mécanique analytique, joue également un rôle clé. Il utilise le principe de moindre action pour déterminer la trajectoire d’une particule.

Dans ce contexte, la force de Lorentz est déduite à partir des variations de l’action, qui est une mesure de l’énergie dynamique du système. Les équations de mouvement des particules chargées dans des champs électromagnétiques sont ainsi obtenues en appliquant ce formalisme.

Ces implications théoriques ne sont pas de simples exercices académiques. Elles permettent de mieux comprendre des phénomènes complexes comme les champs électromagnétiques dans les trous noirs ou les particules à des vitesses proches de celle de la lumière.

En somme, la force de Lorentz, lorsqu’examinée à travers le prisme de la relativité et du formalisme Lagrangien, révèle des aspects fascinants et fondamentaux de notre univers.

Conclusion

En parcourant les différentes facettes de la force de Lorentz, nous avons exploré un concept qui se révèle être un joyau de la physique.

De sa définition élémentaire à ses implications profondes en électrodynamique quantique et relativité restreinte, la force de Lorentz se dresse comme un pilier central dans notre compréhension de l’univers.

Elle est un parfait exemple de l’interconnexion des phénomènes naturels, reliant les théories classiques aux frontières de la physique moderne.

La richesse de ce sujet ne réside pas seulement dans son importance académique, mais aussi dans son impact tangible sur la technologie, la médecine et la recherche scientifique.

En définitive, la force de Lorentz incarne la beauté et la complexité de la physique, un domaine en constante évolution, qui continue de façonner notre vision du monde et de l’univers.