Loi des Sinus : Le Guide Complet de la Trigonométrie

La loi des sinus, pierre angulaire de la trigonométrie, se révèle essentielle dans la compréhension des relations géométriques des triangles.

Cet article explore cette loi fondamentale, offrant une vision claire de ses applications et implications.

De son origine historique à son utilisation moderne, nous dévoilerons les secrets de cette formule puissante.

La loi des sinus ne se limite pas aux salles de classe ; elle joue un rôle crucial en navigation, en astronomie et dans divers domaines scientifiques.

Notre objectif est de démystifier cette loi, en présentant ses concepts de manière accessible.

Qu’est ce que la loi des sinus ?

La loi des sinus, concept fondamental en trigonométrie, offre un lien précis entre les angles et les côtés d’un triangle.

Elle établit que le rapport entre la longueur d’un côté et le sinus de son angle opposé est constant pour tous les côtés du triangle.

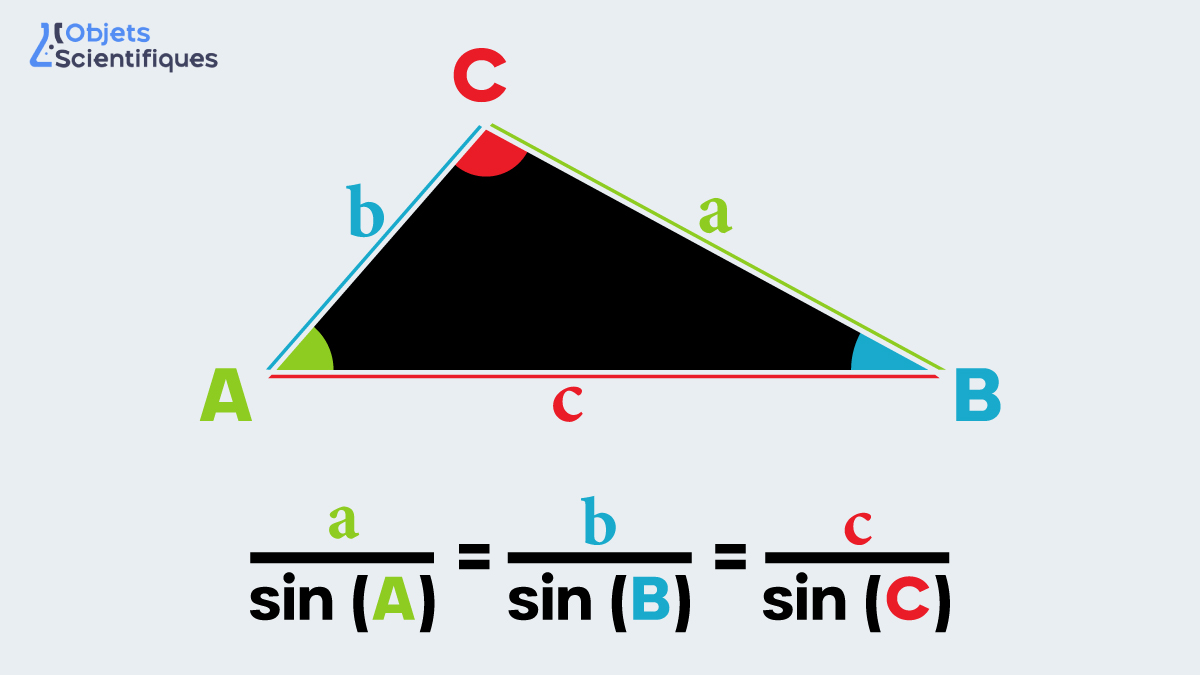
Formulée mathématiquement, la loi des sinus se présente ainsi :

sin(alpha) / a = sin(beta) / b = sin(gamma) / c

Dans cette formule, sin(alpha), sin(beta), et sin(gamma) représentent les sinus des angles α, β, et γ, respectivement, tandis que a, b, et c sont les longueurs des côtés opposés à ces angles dans un triangle.

Son importance est incontestable. Elle permet de résoudre des triangles non droits, ce qui est crucial en navigation, en astronomie et dans diverses applications scientifiques.

Historiquement, la loi des sinus a été mise en lumière par des mathématiciens arabes médiévaux, notamment Abu Nasr Mansur et Nasir al-Din al-Tusi.

Leur travail a pavé la voie à la compréhension moderne des relations trigonométriques, essentielles dans de nombreux domaines scientifiques.

Fondements Théoriques

Avant de plonger dans la loi des sinus, comprenons les bases de la trigonométrie. Elle étudie les relations entre angles et côtés dans les triangles. Le sinus d’un angle, pierre angulaire de cette loi, est un rapport.

Dans un triangle rectangle, il correspond au rapport entre la longueur du côté opposé à l’angle et la longueur de l’hypoténuse.

Un angle est formé par l’intersection de deux droites ou segments. Dans un triangle, les angles sont souvent désignés par des lettres grecques comme $\alpha$, $\beta$, et $\gamma$. Chaque angle a un côté opposé, situé en face de lui.

Par exemple, le côté opposé à l’angle $\alpha$ est le côté qui ne touche pas directement cet angle.

Ces éléments constituent la base pour comprendre la loi des sinus, un outil puissant pour résoudre divers problèmes géométriques et trigonométriques.

Énoncé de la Loi des Sinus

La loi des sinus se formule ainsi : pour tout triangle $ABC$, les rapports entre la longueur d’un côté et le sinus de son angle opposé sont égaux. En mathématique, cela s’exprime par :

asin⁡(α)=bsin⁡(β)=csin⁡(γ)sin(α)a​=sin(β)b​=sin(γ)c​

Ici, $a$, $b$, et $c$ désignent les longueurs des côtés du triangle, et $\alpha$, $\beta$, $\gamma$ sont les angles opposés à ces côtés respectivement. Ce principe trouve une application concrète dans la résolution de triangles non droits, où au moins un angle et un côté opposé sont connus.

Pour illustrer, considérons un triangle $ABC$ où $a$ est le côté opposé à l’angle $\alpha$, $b$ le côté opposé à $\beta$, et $c$ le côté opposé à $\gamma$.

Cette équation nous permet de déduire la mesure d’un côté ou d’un angle inconnu, dès lors qu’une paire côté-angle est connue, avec un autre élément supplémentaire.

Pourquoi utiliser la Loi des Sinus ?

La loi des sinus est inestimable pour résoudre des triangles quelconques. Elle permet de calculer les longueurs des côtés et les mesures des angles sans se limiter aux triangles rectangles. Ainsi, elle devient un outil polyvalent en trigonométrie.

Prenons un exemple concret : supposons un triangle avec des côtés de longueurs $a$ et $b$, et un angle $\alpha$ connu opposé à $a$. Si nous connaissons $b$ et souhaitons trouver $\beta$, l’angle opposé à $b$, la loi des sinus nous permet de le faire aisément. On applique :

asin⁡(α)=bsin⁡(β)sin(α)a​=sin(β)b​

En réarrangeant, on trouve $\beta$ :

β=sin⁡−1(b⋅sin⁡(α)a)β=sin−1(ab⋅sin(α)​)

Cet exemple illustre l’efficacité de la loi des sinus dans la détermination d’éléments inconnus d’un triangle, rendant les calculs en trigonométrie plus accessibles et diversifiés.

Cas Particuliers et Limitations

La loi des sinus brille dans sa flexibilité, s’appliquant tant aux triangles obtus qu’aux triangles aigus. Elle permet de résoudre un large éventail de triangles, mais avec certaines précautions.

Dans les triangles obtus, un angle dépasse 90°. Ici, la loi des sinus reste valide, mais une attention particulière est nécessaire lors du calcul des angles, pour éviter les ambiguïtés dues à la fonction sinus.

En effet, le sinus d’un angle obtus est égal à celui de son angle supplémentaire, ce qui peut entraîner des confusions.

Pour les triangles aigus, où tous les angles sont inférieurs à 90°, l’application est plus directe. Cependant, la loi des sinus peut présenter des limitations. L’une des principales est le cas d’ambiguïté.

Lorsqu’on connaît un côté et son angle opposé, il peut exister deux triangles différents respectant ces conditions. Ce phénomène se produit lorsque l’angle connu est aigu et le côté opposé est plus court que le côté connu.

Extension de la Loi des Sinus

La loi des sinus s’étend au-delà de la trigonométrie plane, trouvant une application pertinente en trigonométrie sphérique. Cette extension est cruciale pour étudier les figures sur des surfaces courbes, comme les sphères.

En trigonométrie sphérique, la loi des sinus relie les angles d’un triangle sphérique et les arcs des grands cercles qui forment ses côtés.

La formule s’adapte pour des angles et des arcs mesurés en degrés ou radians sur la sphère. Elle est ainsi formulée :

sin⁡(a)sin⁡(A)=sin⁡(b)sin⁡(B)=sin⁡(c)sin⁡(C)sin(A)sin(a)​=sin(B)sin(b)​=sin(C)sin(c)​

Ici, $a$, $b$, et $c$ sont les longueurs des arcs des grands cercles, et $A$, $B$, $C$ sont les angles du triangle sphérique.

La comparaison avec la trigonométrie plane révèle une adaptabilité remarquable de la loi. En trigonométrie plane, la loi des sinus s’applique aux triangles plats sur des surfaces planes.

En revanche, sa version sphérique prend en compte la courbure de la sphère, offrant ainsi une précision indispensable en astronomie et en navigation globale.

Démonstration de la Loi des Sinus

La loi des sinus se démontre de manière élégante à travers une approche géométrique. Cette démonstration souligne la relation profonde entre la structure d’un triangle et ses propriétés trigonométriques.

Considérons un triangle $ABC$ avec une hauteur $h$ tombant du sommet $C$ sur la base $AB$. Cette hauteur divise le triangle en deux triangles rectangles, $AHC$ et $BHC$. En utilisant le sinus, on peut exprimer la hauteur $h$ de deux façons :

1. $h=b\cdot \sin (\alpha )$ dans le triangle $AHC$
2. $h=a\cdot \sin (\beta )$ dans le triangle $BHC$

En égalisant ces deux expressions, nous obtenons :

$b\cdot \sin (\alpha )=a\cdot \sin (\beta )$

En réarrangeant, on aboutit à la forme classique de la loi des sinus pour deux côtés et leurs angles opposés :

asin⁡(α)=bsin⁡(β)sin(α)a​=sin(β)b​

La relation avec l’aire du triangle est également révélatrice. L’aire $S$ de $ABC$ peut être exprimée en utilisant la base $AB$ et la hauteur $h$ :

S=12⋅AB⋅hS=21​⋅AB⋅h

En remplaçant $h$ par $b\cdot \sin (\alpha )$ et $AB$ par $c$, on obtient :

S=12⋅c⋅b⋅sin⁡(α)S=21​⋅c⋅b⋅sin(α)

Importance Historique et Contributions Clés

L’histoire de la loi des sinus est riche, marquée par des contributions significatives de mathématiciens éminents. Son évolution reflète l’avancée des connaissances en géométrie et trigonométrie à travers les âges.

Le concept de base, liant les côtés d’un triangle à ses angles, trouve ses racines dans l’Antiquité. Cependant, c’est au Moyen Âge que la loi prend sa forme actuelle.

Des mathématiciens du monde islamique, comme Abu Nasr Mansur et Nasir al-Din al-Tusi, ont joué un rôle crucial dans cette évolution. Leurs travaux ont non seulement formalisé la loi des sinus dans le contexte des triangles plans, mais aussi établi ses fondements en trigonométrie sphérique.

Ces avancées ont eu un impact majeur sur la navigation et l’astronomie, disciplines où la compréhension précise des angles et distances est vitale.

Leurs contributions ont ainsi pavé la voie aux découvertes ultérieures en Europe et ailleurs, influençant des générations de scientifiques et mathématiciens. La loi des sinus reste un témoignage de l’interconnexion des cultures dans l’histoire des sciences.

Applications Pratiques de la Loi des Sinus

La loi des sinus s’avère cruciale dans de nombreux domaines pratiques, notamment en navigation et astronomie. En navigation, elle aide à calculer des angles et des distances, éléments vitaux pour la navigation maritime et aérienne.

Les navigateurs l’utilisent pour déterminer la route la plus directe entre deux points, en tenant compte de la courbure de la Terre.

En astronomie, cette loi permet de mesurer des distances inaccessibles. Elle aide les astronomes à calculer les distances des étoiles et des planètes en se basant sur des angles observés depuis la Terre.

Cette capacité à mesurer l’immensité spatiale repose en grande partie sur la loi des sinus.

Dans le domaine de l’ingénierie, cette loi trouve des applications dans la conception de structures et la résolution de problèmes géométriques complexes.

Elle aide les ingénieurs à calculer des forces et des contraintes dans diverses structures, telles que les ponts ou les bâtiments.

En physique, la loi des sinus est utilisée pour analyser des phénomènes impliquant des forces et des mouvements sous différents angles. Elle permet de comprendre des situations allant de la mécanique simple à la dynamique des fluides.

Exercice : Application de la Loi des Sinus

Énoncé

Dans un triangle $ABC$, les longueurs des côtés sont $AB=8$ unités et $AC=6$ unités. L’angle BAC^BAC

(angle $A$) mesure 60∘60∘. Utilisez la loi des sinus pour trouver la mesure de l’angle BCA^BCA

(angle $C$).

Indice

Appliquez la loi des sinus sous la forme :

asin⁡(α)=csin⁡(γ)sin(α)a​=sin(γ)c​

Ici, $a=6$ (côté $AC$), α=60∘α=60∘ (angle $A$), et $c=8$ (côté $AB$). Calculez $\sin (\gamma )$ pour trouver l’angle $\gamma$ (angle $C$).

Résultat

En réarrangeant la formule, on obtient :

sin⁡(γ)=c⋅sin⁡(α)a=8⋅sin⁡(60∘)6sin(γ)=ac⋅sin(α)​=68⋅sin(60∘)​

En calculant, on trouve :

$\sin (\gamma )\approx 0,9239$

En prenant l’arc sinus, l’angle $\gamma$ (angle $C$) est approximativement :

γ≈67,38∘γ≈67,38∘

Cet exercice illustre comment la loi des sinus aide à déterminer les angles inconnus dans un triangle non rectangle.

Conclusion

En somme, la loi des sinus s’avère être un outil mathématique d’une remarquable versatilité et puissance. Sa capacité à relier angles et côtés dans divers types de triangles en fait une pierre angulaire de la trigonométrie.

Sa portée, s’étendant de la résolution de problèmes géométriques complexes à des applications pratiques en sciences et ingénierie, témoigne de son importance fondamentale.

À travers l’histoire, ses contributions au développement de disciplines telles que la navigation et l’astronomie soulignent son rôle inestimable dans l’avancement des connaissances humaines.

La loi des sinus, loin d’être un simple concept théorique, est un pilier essentiel dans notre compréhension du monde qui nous entoure.