Lois de Kirchhoff : Conservation de l’Énergie et de la Charge en Électrocinétique

Les lois de Kirchhoff expriment la conservation de l’énergie et de la charge dans un circuit électrique.

Elles permettent de calculer les différences de potentiel et les intensités de courant dans les circuits complexes.

Établies en 1845 par le physicien allemand Gustav Kirchhoff, ces lois sont essentielles pour l’analyse des circuits électriques.

Qu’est ce que les lois de Kirchhoff ?

Les lois de Kirchhoff se composent de deux principes : la loi des nœuds et la loi des mailles. La loi des nœuds stipule que la somme des courants entrant dans un nœud est égale à la somme des courants sortant du même nœud.

La loi des mailles affirme que la somme des différences de potentiel le long d’une maille fermée est nulle. Ces lois utilisent la conservation de l’énergie et de la charge pour décrire le comportement des circuits électriques.

Gustav Kirchhoff, né en 1824 en Allemagne, a formulé ces lois en 1845. À cette époque, la compréhension des circuits électriques était en pleine expansion. Les travaux de Kirchhoff ont permis des avancées significatives dans l’analyse et la conception des circuits électriques.

Ses lois sont devenues des outils fondamentaux pour les ingénieurs et les scientifiques du monde entier.

Principes Fondamentaux

Conservation de l’énergie et de la charge

Les lois de Kirchhoff reposent sur deux principes essentiels : la conservation de l’énergie et la conservation de la charge. La conservation de la charge stipule que la charge électrique totale dans un circuit fermé reste constante.

Les charges ne peuvent ni être créées ni détruites. Elles se déplacent simplement d’un point à un autre.

La conservation de l’énergie affirme que l’énergie totale dans un circuit fermé demeure constante. L’énergie électrique se répartit entre les différentes branches du circuit en fonction de leur impédance.

Cela permet de déterminer les différences de potentiel et les courants dans chaque branche.

Analogies intuitives

Pour mieux comprendre ces principes, on peut utiliser des analogies intuitives. Imaginez un réseau de canaux remplis d’eau. La conservation de la charge est similaire à la conservation du volume d’eau. L’eau entrant dans un canal doit équivaloir à l’eau sortant de ce canal.

De même, la conservation de l’énergie peut être comparée à la répartition de l’eau selon la largeur des canaux. L’eau se répartit en fonction de la capacité de chaque canal, tout comme l’énergie électrique se divise en fonction de l’impédance des branches du circuit.

Loi des Nœuds (Première Loi de Kirchhoff)

La loi des nœuds stipule que la somme des courants entrant dans un nœud est égale à la somme des courants sortant de ce nœud. Cela découle de la conservation de la charge, qui affirme que les charges ne peuvent s’accumuler en un point.

En d’autres termes, ce qui entre doit sortir.

Application de la Loi des Nœuds

Pour appliquer cette loi, on choisit un nœud dans le circuit. Ensuite, on additionne les courants entrants et sortants. En régime stationnaire, cette somme doit être nulle.

Cette méthode permet de résoudre des systèmes d’équations électriques et de déterminer les courants inconnus dans le circuit.

Exemple Pratique

Considérons un nœud avec quatre branches. Les courants entrants sont i1 et i2. Les courants sortants sont i3 et i4. Selon la loi des nœuds :

i1 + i2 = i3 + i4

Imaginons que i1 = 3 A, i2 = 2 A, et i3 = 4 A. Nous pouvons trouver i4 :

3 + 2 = 4 + i4
5 = 4 + i4
i4 = 1 A

Donc, i4 = 1 A.

Schéma Illustratif

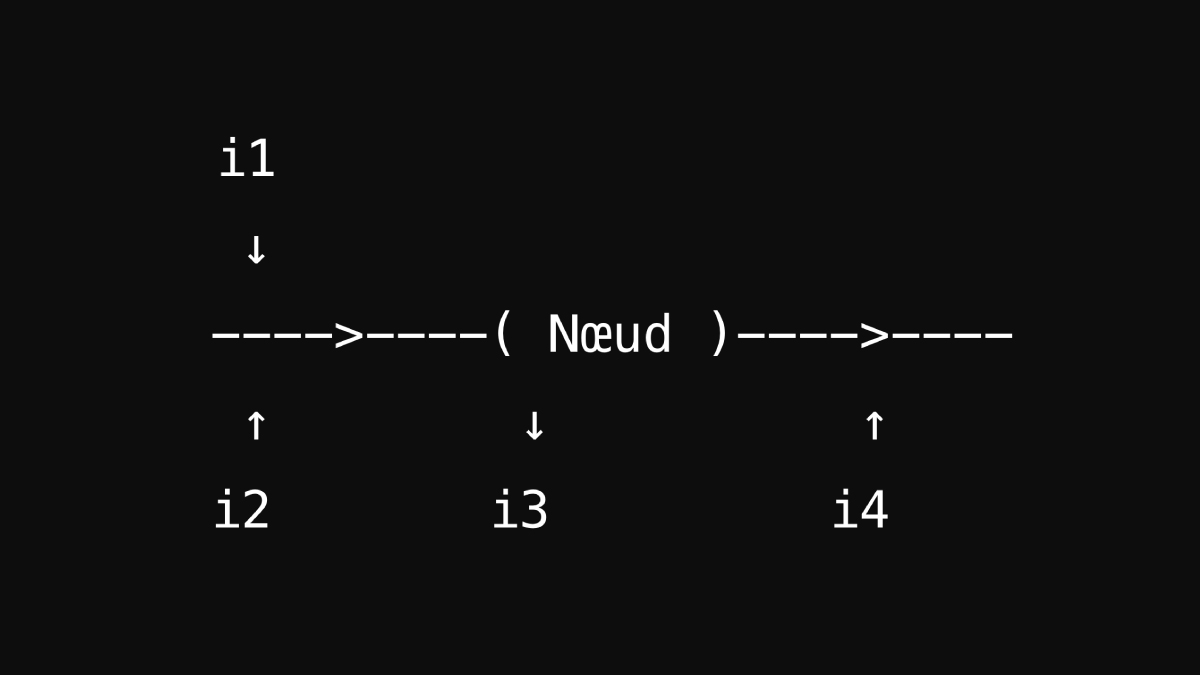
Dans cet exemple, les courants sont balancés comme prévu par la loi des nœuds.

Loi des Mailles (Deuxième Loi de Kirchhoff)

La loi des mailles stipule que la somme des différences de potentiel dans une maille fermée est nulle.

Autrement dit, dans une boucle fermée, la somme des tensions doit égaler zéro. Cette loi découle de la conservation de l’énergie.

Application de la Loi des Mailles

Pour appliquer cette loi, on choisit une maille dans le circuit. Ensuite, on additionne toutes les tensions en tenant compte de leur signe.

Cette méthode aide à trouver les tensions inconnues et à résoudre les équations du circuit.

Exemple Pratique

Considérons une maille avec quatre éléments ayant des tensions Uab, Ubc, Ucd et Uda. Selon la loi des mailles :

Uab + Ubc + Ucd + Uda = 0

Imaginons les valeurs suivantes : Uab = 5 V, Ubc = −3 V, Ucd = −2 V. Nous devons trouver Uda :

5 + (−3) + (−2) + Uda = 0
5 − 3 − 2 + Uda = 0
Uda = 0

Schéma Illustratif

Dans cet exemple, la somme des tensions autour de la maille est nulle, confirmant la loi des mailles.

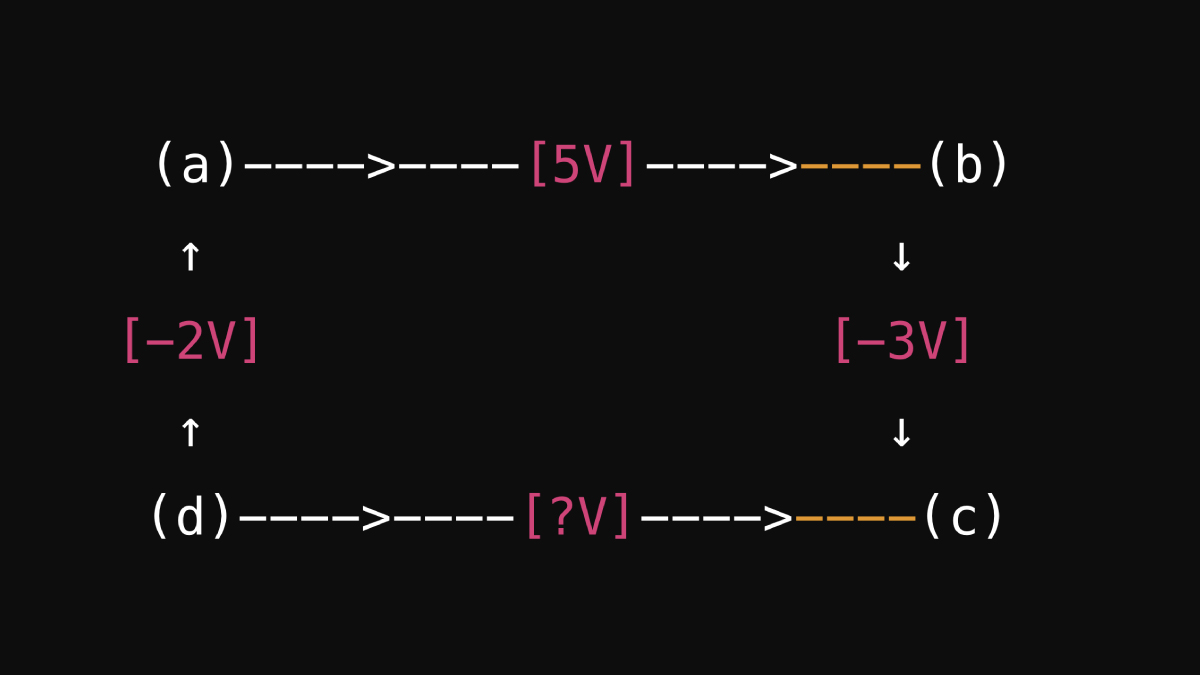
Limitations et Conditions de Validité

Limites de la loi des nœuds en électrostatique

La loi des nœuds présente des limites en électrostatique. En effet, elle suppose que les charges ne s’accumulent pas en un point du circuit.

Cependant, en électrostatique, le stockage ou la production de charges statiques peut modifier localement le bilan énergétique.

Cela rend l’application stricte de la loi des nœuds inadéquate. Par conséquent, les solutions obtenues ne sont pas toujours fiables.

Validité des lois dans différents contextes

Les lois de Kirchhoff restent valides dans la plupart des circuits électriques en régime permanent. Elles s’appliquent efficacement aux circuits linéaires où les composants respectent les conditions stationnaires.

Toutefois, elles montrent leurs limites dans les circuits à haute fréquence et ceux avec des variations rapides de flux magnétique.

En électrodynamique, les effets inductifs et capacitifs deviennent significatifs. Ici, les lois de Kirchhoff doivent être adaptées ou complétées par d’autres équations.

De même, dans les circuits avec des composants non linéaires comme les diodes et les transistors, les approximations doivent être ajustées pour une analyse précise.

Application aux Semi-conducteurs

Comportement des Charges Mobiles

Dans un semi-conducteur, deux types de charges mobiles coexistent : les électrons et les trous. Le courant total résulte de la somme des courants des électrons et des trous. La loi des nœuds s’applique strictement à ces courants.

Les électrons se déplacent vers les potentiels positifs, tandis que les trous se dirigent vers les potentiels négatifs.

Application aux Transistors Bipolaires

Dans un transistor bipolaire, le courant est principalement dû aux porteurs minoritaires dans la base. La loi des nœuds aide à modéliser ce comportement.

En tenant compte du stockage et de la recombinaison des porteurs, on peut prédire le fonctionnement du transistor. Cette approche permet de comprendre le gain de courant et la fréquence de transition du transistor.

Équation Améliorée pour les Transistors-Laser

Pour les transistors-laser, une équation améliorée de Kirchhoff s’avère nécessaire. Cette équation inclut les effets de recombinaison radiative et non-radiative.

Elle décrit avec précision le comportement optoélectronique des transistors-laser. Ainsi, elle permet d’optimiser leur performance en termes de puissance de sortie et d’efficacité quantique.

Cette équation a suscité un vif intérêt dans la recherche en photonique.

Conclusion

Les lois de Kirchhoff sont essentielles pour analyser et comprendre les circuits électriques complexes. Elles permettent de déterminer les courants et les tensions en utilisant des principes simples de conservation de l’énergie et de la charge.

Leur application s’étend aux circuits linéaires et non linéaires, y compris les composants avancés comme les semi-conducteurs et les transistors. Bien que des ajustements soient nécessaires dans certains contextes, leur utilité reste indéniable.

Ces lois fournissent une base solide pour l’étude et la conception de systèmes électroniques. Elles sont indispensables pour les étudiants, les ingénieurs et les chercheurs.

En maîtrisant les lois de Kirchhoff, on peut résoudre efficacement une grande variété de problèmes en électrotechnique et en électronique.

Références

Bibliographie et Sources Utilisées

Pour approfondir les lois de Kirchhoff, consultez les ouvrages suivants :

1. J. E. Whitehouse, Circuit Analysis, Elsevier Science, 1997. ISBN 978-1-898563-40-2.
2. Christophe Palermo et Jérémie Torres, Électricité, Dunod, juin 2022. ISBN 978-2-10-080933-2.

Ces livres fournissent des explications détaillées et des exemples pratiques. Ils sont essentiels pour comprendre l’application des lois de Kirchhoff dans l’analyse des circuits électriques.

Références pour Approfondir le Sujet

Pour en savoir plus, explorez les ressources en ligne suivantes :

1. Khan Academy – Les lois de Kirchhoff
2. Leçon sur les lois de Kirchhoff – Application pratique

Ces références offrent des vidéos et des exercices interactifs pour renforcer votre compréhension des concepts clés. Utilisez ces ressources pour une étude approfondie et interactive des lois de Kirchhoff.