Loi de Cauchy : Comprendre Sa Dynamique et Ses Applications

La loi de Cauchy, également connue sous le nom de loi de Lorentz, est une distribution de probabilités continue.

Cette loi tient son nom du mathématicien Augustin Louis Cauchy. Elle se distingue par ses queues lourdes et son absence de moyenne ou de variance définie, ce qui la rend unique par rapport aux distributions plus courantes comme la loi normale.

En raison de ces propriétés, la loi de Cauchy est particulièrement utile dans les domaines où les valeurs extrêmes sont fréquentes, tels que la physique quantique et certains types d’analyses financières.

Qu’est-ce que la loi de Cauchy?

Définition et Contexte Historique

La loi de Cauchy, aussi appelée loi de Lorentz, est une distribution de probabilités continue qui se caractérise par une densité de forme lorentzienne.

Nom donné en honneur à Augustin Louis Cauchy, cette loi émerge souvent dans les résultats impliquant des rapports de variables aléatoires normalement distribuées.

Introduite dans les années 1820, elle se distingue des autres distributions par son absence de moyenne et de variance définies.

Importance en Statistique et Physique

En statistique, la loi de Cauchy challenge les méthodes standard d’analyse en raison de ses queues lourdes et de l’absence d’indicateurs centraux stables.

Elle souligne l’importance de comprendre les distributions avant d’appliquer des outils analytiques. En physique, cette distribution est cruciale pour décrire des phénomènes comme la dispersion de la lumière et les profils d’émission en spectroscopie.

Elle aide à modéliser des situations où les événements extrêmes sont plus fréquents que ne le suggère la loi normale, rendant la loi de Cauchy indispensable dans les théories de la mécanique quantique et de la théorie des champs.

Caractérisation de la Loi de Cauchy

Densité de Probabilités

La densité de probabilités de la loi de Cauchy est définie par la formule :

$f(x;x_0,a)=\frac{1}{\pi a[1+{\left(\frac{x-x_0}{a}\right)}^2]}$

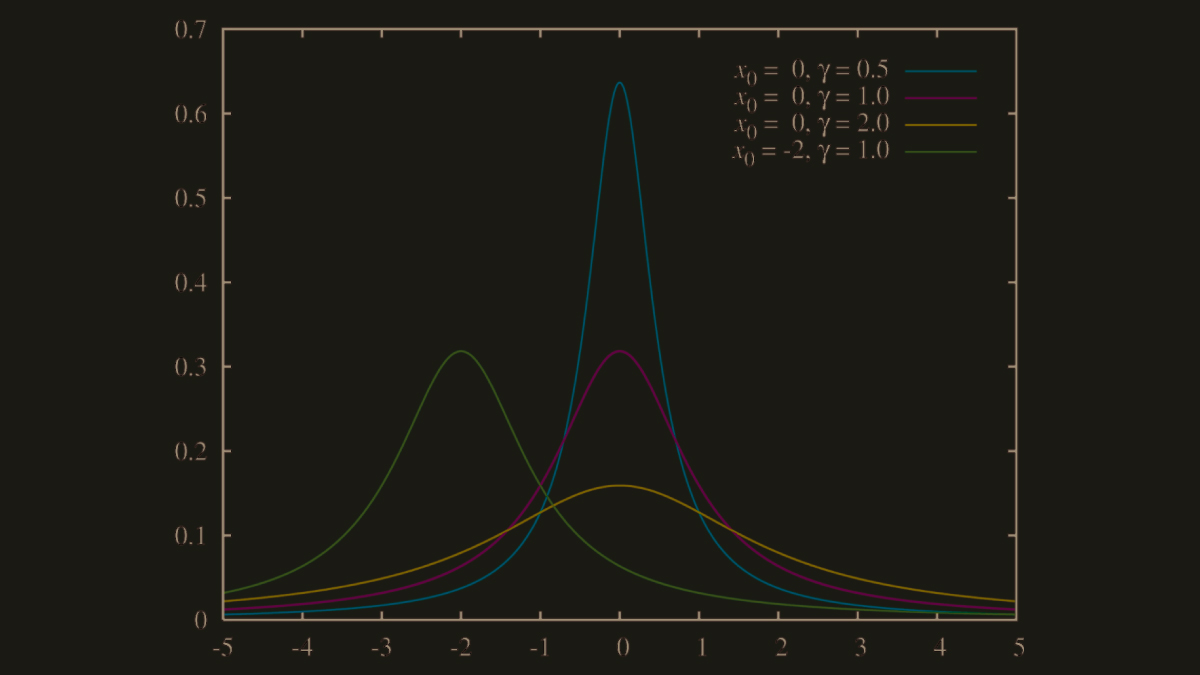
x0​ est le paramètre de position et a est le paramètre d’échelle. Cette densité lorentzienne possède un pic central à x0​ et s’étale symétriquement avec des queues qui ne diminuent jamais complètement, indiquant une probabilité non-négligeable pour les valeurs extrêmes.

Fonction de Répartition

La fonction de répartition pour la loi de Cauchy s’exprime comme :

$F(x;x_0,a)=\frac{1}{2}+\frac{1}{\pi }\arctan \left(\frac{x-x_0}{a}\right)$

Elle illustre comment les probabilités cumulées se distribuent le long de l’axe des réels, transitionnant en douceur d’un minimum à un maximum sans points de discontinuité.

Entropie

L’entropie de la loi de Cauchy, qui mesure l’incertitude inhérente à la distribution, se calcule par :

$H(a)=\ln (4\pi a)$

Cette valeur élevée d’entropie reflète la grande variabilité et l’imprévisibilité des issues d’une variable aléatoire suivant cette loi.

Fonction Caractéristique

La fonction caractéristique offre une perspective sur le comportement des transformées de Fourier de la loi. Pour la loi de Cauchy, elle se formule comme :

${\phi }_X(t)=e^{i{x}_{0}t-a\mathrm{\mid }t\mathrm{\mid }}$

ce qui souligne la façon dont la loi gère les fluctuations à différentes échelles. Cette fonction est cruciale pour comprendre la structure interne de la distribution et pour le développement de méthodes analytiques avancées.

Propriétés Statistiques de la Loi de Cauchy

Absence d’Espérance et d’Écart Type

La loi de Cauchy se distingue par l’absence d’espérance et d’écart type. Les intégrales nécessaires pour calculer ces statistiques ne convergent pas.

Cette particularité met en évidence la nature imprévisible de la distribution. Les valeurs extrêmes ont un impact significatif, empêchant toute moyenne stable.

Ce trait rend la loi de Cauchy unique, défiant les méthodes statistiques traditionnelles basées sur ces indicateurs.

Médiane et Mode

Contrairement à l’espérance, la médiane de la loi de Cauchy est bien définie et correspond au paramètre de position ${}_{}$x0​. Le mode, qui représente le point le plus fréquent de la distribution, coïncide également avec ${}_{}$x0​.

Ces indicateurs de tendance centrale offrent une certaine prévisibilité dans une distribution autrement imprévisible. Ils sont souvent utilisés pour résumer la loi de Cauchy, fournissant un point de référence autour duquel les valeurs sont symétriquement distribuées.

Comparaison de la Loi de Cauchy avec d’Autres Lois

Loi de Cauchy vs Loi Normale

La loi de Cauchy diffère de la loi normale de plusieurs manières cruciales. Contrairement à la loi normale, qui possède des moyennes et des variances bien définies, la loi de Cauchy n’a ni espérance mathématique, ni écart type.

Cela est dû à ses queues lourdes, qui influencent les calculs de ces paramètres. En statistique, alors que la loi normale bénéficie de la propriété de convergence rapide vers la moyenne avec un échantillon croissant, la loi de Cauchy reste imprévisible, la moyenne d’un échantillon n’ayant pas de valeur centrale stable.

Cette caractéristique rend la loi normale adaptée aux phénomènes naturels courants, tandis que la loi de Cauchy est préférée pour modéliser des scénarios où les valeurs extrêmes sont fréquentes.

Cas Particulier de Loi Stable

La loi de Cauchy est un exemple de loi stable, un groupe de distributions utilisé pour modéliser des données avec des comportements extrêmes ou atypiques.

Toutes les lois stables sont paramétrées par un indice de stabilité, et pour la loi de Cauchy, cet indice est 1. Cela signifie qu’elle conserve sa forme sous addition de variables indépendantes identiquement distribuées.

D’autres lois stables incluent la loi normale, avec un indice de stabilité de 2, offrant une plus grande flexibilité pour modéliser différents types de données.

La loi de Cauchy, avec sa capacité à modéliser des données avec de lourdes queues, sert souvent dans des domaines où les modèles normaux ne suffisent pas.

Applications Pratiques de la Loi de Cauchy

Utilisation en Spectroscopie

En spectroscopie, la loi de Cauchy est essentielle pour modéliser la forme des raies d’émission et d’absorption. Sa densité lorentzienne capture précisément la distribution de l’intensité lumineuse autour d’une fréquence centrale.

Ce profil est crucial pour analyser les spectres lumineux des étoiles et autres sources lumineuses, où les effets de largeur naturelle et de pression modifient les fréquences observées.

Cette application démontre la capacité de la loi de Cauchy à traiter des phénomènes où les événements extrêmes, comme les déviations spectrale significatives, sont probables.

Exemple en Finance et en Physique

En finance, la loi de Cauchy aide à comprendre les comportements de marché extrêmes, comme les sauts brutaux des prix des actions. Sa distribution avec des queues lourdes offre un meilleur modèle que la loi normale pour ces événements rares mais influents.

En physique, cette loi s’applique dans l’étude des phénomènes de dispersion et de propagation d’ondes, où des valeurs extrêmes peuvent dominer les dynamiques observées.

Théorèmes et Propriétés Mathématiques de la Loi de Cauchy

Rapport de Vraisemblance Monotone

La loi de Cauchy présente un cas unique où le rapport de vraisemblance n’est pas monotone. Cela signifie que la probabilité relative de deux observations ne suit pas toujours un ordre croissant ou décroissant strict.

Cette particularité complique l’utilisation de méthodes statistiques standard, comme les tests d’hypothèses, qui dépendent souvent de la monotonie pour déterminer des seuils de significativité.

Elle souligne la nécessité d’approches spécifiques pour analyser les données soumises à cette loi.

Implications des Théorèmes Limite

Contrairement à d’autres distributions, la loi de Cauchy ne se conforme pas au théorème central limite.

Ce principe fondamental stipule que la moyenne d’un échantillon de variables indépendantes et identiquement distribuées tend vers une distribution normale à mesure que la taille de l’échantillon augmente.

Pour la loi de Cauchy, la moyenne d’un échantillon reste distribuée selon une loi de Cauchy, quel que soit le nombre d’observations.

Cela a des implications profondes pour la modélisation statistique, notamment le fait que les méthodes basées sur la moyenne ou la variance sont inapplicables.

Qui est Augustin-Louis Cauchy ?

Biographie Succincte

Augustin-Louis Cauchy, né le 21 août 1789 à Paris, est un mathématicien français éminent. Issu d’une famille modeste, son parcours académique débute brillamment à l’École Polytechnique puis à l’École des Ponts et Chaussées.

Sa carrière est marquée par une fuite en avant durant les troubles politiques de la France, ce qui l’amène à voyager à travers l’Europe.

Dévoué à ses convictions religieuses et politiques, Cauchy ne cède jamais sur ses principes, ce qui influence tant sa vie personnelle que professionnelle.

Contributions à la Mathématique

Cauchy a révolutionné plusieurs domaines des mathématiques, y compris l’analyse, les séries, les équations différentielles, et la théorie des groupes.

Il est particulièrement reconnu pour avoir formalisé le concept de limite et pour ses travaux sur la continuité des fonctions.

Cauchy a aussi établi de nombreux théorèmes fondamentaux, comme le théorème des résidus en analyse complexe et le théorème de Cauchy-Lipschitz pour les équations différentielles.

Son approche rigoureuse a jeté les bases de l’analyse moderne, influençant profondément les générations suivantes de mathématiciens.

Ses contributions ont non seulement enrichi la théorie mathématique mais aussi amélioré les méthodes d’enseignement des mathématiques à travers le monde.

Notes et Références

Pour approfondir la compréhension de la Loi de Cauchy et des contributions d’Augustin-Louis Cauchy aux mathématiques, les sources suivantes peuvent être consultées :

1. N. L. Johnson, S. Kotz, et N. Balakrishnan, Continuous Univariate Distributions, Volume 1. Cet ouvrage offre un examen détaillé des distributions univariées, y compris la loi de Cauchy.
2. William Feller, An Introduction to Probability Theory and Its Applications, Volume II. Ce livre classique fournit une introduction fondamentale à la théorie des probabilités, avec des discussions spécifiques sur des distributions telles que la loi de Cauchy.
3. Sung Y. Park et Anil K. Bera, « Maximum entropy autoregressive conditional heteroskedasticity model ». Un article explorant les applications de la théorie de l’entropie maximale dans les modèles économétriques, pertinent pour comprendre l’entropie de la loi de Cauchy.
4. Jean Pierre Lecoutre, Statistique et probabilités. Ce livre contient des informations pertinentes sur l’utilisation et les propriétés de la loi de Cauchy dans le contexte statistique.
5. Des articles de revue et des chapitres de livres concernant Augustin-Louis Cauchy et son impact sur les développements en analyse, disponibles dans les archives de diverses académies de sciences.